О приближениях одного сингулярного интеграла на отрезке рациональными интегральными операторами Фурье–Чебышёва
https://doi.org/10.29235/1561-8323-2024-68-2-95-104
Анатацыя
Исследуются рациональные аппроксимации на отрезке [–1, 1] сингулярных интегралов вида 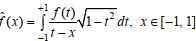 , интегральными операторами, в некотором смысле связанными между собой. Первый из них – рациональный интегральный оператор Фурье–Чебышёва, ассоциированный с системой рациональных функций Чебышёва–Маркова. Он является естественным обобщением частичных сумм полиномиального ряда Фурье–Чебышёва. Второй оператор является образом первого при преобразовании исследуемым сингулярным интегралом. Для каждого из операторов установлено интегральное представление приближений. Изучаются аппроксимации на отрезке [–1, 1] сингулярного интеграла с плотностью, имеющей степенную особенность. Для каждого из операторов рассматривается случай произвольного фиксированного количества геометрически различных полюсов и случай, когда полюсы представляют собой некоторые модификации «ньюменовских» параметров. Установлено, что классы изучаемых сингулярных интегралов отражают особенности рациональной аппроксимации рассматриваемыми интегральными операторами в том смысле, что при специальном выборе параметров аппроксимирующих функций порядки их приближений оказываются выше соответствующих полиномиальных аналогов.
, интегральными операторами, в некотором смысле связанными между собой. Первый из них – рациональный интегральный оператор Фурье–Чебышёва, ассоциированный с системой рациональных функций Чебышёва–Маркова. Он является естественным обобщением частичных сумм полиномиального ряда Фурье–Чебышёва. Второй оператор является образом первого при преобразовании исследуемым сингулярным интегралом. Для каждого из операторов установлено интегральное представление приближений. Изучаются аппроксимации на отрезке [–1, 1] сингулярного интеграла с плотностью, имеющей степенную особенность. Для каждого из операторов рассматривается случай произвольного фиксированного количества геометрически различных полюсов и случай, когда полюсы представляют собой некоторые модификации «ньюменовских» параметров. Установлено, что классы изучаемых сингулярных интегралов отражают особенности рациональной аппроксимации рассматриваемыми интегральными операторами в том смысле, что при специальном выборе параметров аппроксимирующих функций порядки их приближений оказываются выше соответствующих полиномиальных аналогов.
Аб аўтарах
П. ПоцейкоБеларусь
Е. Ровба
Беларусь
Спіс літаратуры
1. Гахов, Ф. Д. Краевые задачи / Ф. Д. Гахов. – М., 1958. – 543 с.
2. Мусхелишвили, Н. И. Сингулярные интегральные уравнения. 3-е изд. / Н. И. Мусхелишвили. – М., 1968. – 513 с.
3. Erdogan, F. On the numerical solution of singular integral equations / F. Erdogan, G. D. Gupta // Quarterly of Applied Mathematics. – 1972. – Vol. 29, N 4. – P. 525–534. https://doi.org/10.1090/qam/408277
4. Elliott, D. On the convergence of a quadrature rule for evaluating certain Cauchy principal value integrals / D. Elliott, D. Paget // Numerische Mathematik. – 1974. – Vol. 23, N 4. – P. 311–319. https://doi.org/10.1007/bf01438258
5. Шешко, М. А. О сходимости квадратурных процессов для сингулярного интеграла / М. А. Шешко // Изв. высших учебных заведений. Математика. – 1976. – № 12. – С. 108–118.
6. Саакян, А. В. Квадратурные формулы типа Гаусса для сингулярных интегралов / А. В. Саакян // Проблемы механики тонких деформируемых тел: сб., посвящ. 80-летию акад. С. А. Амбарцумяна. – Ереван, 2002. – C. 259–265.
7. Хубежты, Ш. С. Квадратурные формулы для сингулярных интегралов с ядром Коши / Ш. С. Хубежты // Владикавказский мат. журн. – 2008. – Т. 10, № 4. – С. 61–75.
8. Хубежты, Ш. С. Квадратурные формулы для сингулярных интегралов, имеющих почти гауссовскую степень точности / Ш. С. Хубежты, А. О. Цуцаев // Изв. вузов. Северо-Кавказский рег. Естеств. науки. – 2015. – № 2. – С. 53–57.
9. Русак, В. Н. Равномерная рациональная аппроксимация сингулярных интегралов / В. Н. Русак // Вес. Нац. акад. навук Беларусі. Сер. фіз.-мат. навук. – 1993. – № 2. – С. 22–26.
10. Бокша, А. Н. Приближение сингулярных интегралов рациональными функциями в равномерной метрике / А. Н. Бокша // Вестн. Бел. гос. ун-та. Сер. 1: Физика. Математика. Информатика. – 1997. – № 3. – С. 68–71.
11. Русак, В. Н. Рациональная аппроксимация сингулярных интегралов с дифференцируемой плотностью / В. Н. Русак, А. Х. Уазис // Вес. БДПУ. Сер. 3. Фізіка. Матэматыка. Інфарматыка. Біялогія. Геаграфія. – 2009. – № 1(59). – С. 8–11.
12. Моторный, В. П. Приближение некоторых классов сингулярных интегралов алгебраическими многочленами / В. П. Моторный // Укр. мат. журн. – 2001. – Т. 53, № 3. – С. 331–345.
13. Ровба, Е. А. Об одном прямом методе в рациональной аппроксимации / Е. А. Ровба // Докл. АН БССР. – 1979. – Т. 23, № 11. – С. 968–971.
14. Поцейко, П. Г. Об одном рациональном интегральном операторе типа Фурье–Чебышёва и аппроксимации функций Маркова / П. Г. Поцейко, Е. А. Ровба, К. А. Смотрицкий // Журн. Белорусского гос. ун-та. Математика. Информатика. – 2020. – № 2. – С. 6–27 (на англ. яз.). https://doi.org/10.33581/2520-6508-2020-2-6-27.
15. Поцейко, П. Г. Приближения на классах интегралов Пуассона рациональными интегральными операторами Фурье–Чебышёва / П. Г. Поцейко, Е. А. Ровба // Сибир. мат. журн. – 2021. – Т. 62, № 2. – С. 362–386.
16. Лунгу, К. Н. О наилучших приближениях рациональными функциями с фиксированным числом полюсов / К. Н. Лунгу // Математический сб. – 1971. – Т. 86 (128), № 2 (10). – С. 314–324.
17. Лунгу, К. Н. О наилучших приближениях рациональными функциями с фиксированным числом полюсов / К. Н. Лунгу // Сибир. мат. журн. – 1984. – Т. 15, № 2. – С. 151–160.
18. Newman, D. I. Rational approximation to |x| / D. I. Newman // Michigan Mathematical Journal. – 1964. – Vol. 11, N 1. – P. 11–14. https://doi.org/10.1307/mmj/1028999029
19. Поцейко, П. Г. Об оценках равномерных приближений рациональными интегральными операторами Фурье– Чебышёва при определенном выборе полюсов / П. Г. Поцейко, Е. А. Ровба // Математические заметки. – 2023. – Т. 113, вып. 6. – С. 876–894. https://doi.org/10.4213/mzm13621
20. Поцейко, П. Г. Сопряженный рациональный оператор Фурье–Чебышёва и его аппроксимационные свойства / П. Г. Поцейко, Е. А. Ровба // Изв. вузов. Математика. – 2022. – № 3. – С. 44–60.














































