On approximations of a singular integral on a segment by Fourier–Chebyshevʼs rational integral operators
https://doi.org/10.29235/1561-8323-2024-68-2-95-104
Abstract
Rational approximations on a segment [–1, 1] of singular integrals of the form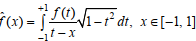 
, by integral operators, in a sense related to each other are studied. The first of them is Fourier–Chebyshev’s rational integral operator associated with the system of Chebyshev–Markov’s rational functions. It is a natural generalization of partial sums of Fourier–Chebyshev’s polynomial series. The second operator is the image of the first one when transformed by a singular integral under study. An integral representation of approximations is established for each of the operators. Approximations on the segment [–1, 1] of a singular integral with a density having a power-law singularity are studied. For each of the operators, we consider the case of an arbitrary fixed number of geometrically different poles and the case when the poles represent some modifications of the “Newman” parameters. It is established that the classes of the studied singular integrals reflect the rational approximation features by the considered integral operators in the sense that with a special choice of parameters of approximating functions, the orders of their approximations turn out to be higher than the corresponding polynomial analogues.
About the Authors
P. G. Potsejko
Yanka Kupala State University of Grodno
Belarus
Belarus
Pavel G. Patseika– Ph. D. (Physics and Mathematics), Associate Professor
22, Ozheshko Str., 230023, Grodno
E. A. Rovba
Yanka Kupala State University of Grodno
Belarus
Belarus
Yevgeniy A. Rovba– D. Sc. (Physics and Mathematics), Professor, Head of the Department
22, Ozheshko Str., 230023, Grodno
References
1. Gakhov F. D. Boundary problems. Moscow, 1958. 543 p. (in Russian).
2. Muskhelishvili N. I. Singular integral equations, 3d ed. Moscow, 1968. 513 p. (in Russian).
3. Erdogan F., Gupta G. D. On the numerical solution of singular integral equations. Quarterly of Applied Mathematics, 1972, vol. 29, no. 4, pp. 525–534. https://doi.org/10.1090/qam/408277
4. Elliott D., Paget D. F. On the convergence of a quadrature rule for evaluating certain Cauchy principal value integrals. Numerische Mathematik, 1974, vol. 23, no. 4, pp. 311–319. https://doi.org/10.1007/bf01438258
5. Sheshko M. A. On the convergence of quadrature processes for a singular integral. Izvestiya vysshikh uchebnykh zavedenii. Matematika = Russian Mathematics, 1976, vol. 12, pp. 108–118 (in Russian).
6. Saakyan A. V. Gauss-type quadrature formulas for singular integrals. Problemy mekhaniki tonkikh deformiruemykh tel: sbornik, posvyashchennyi 80-letiyu akademika S. A. Ambartsumyana [Problems of mechanics of thin deformable bodies: collection dedicated to the 80th anniversary of Academician S. A. Ambartsumyan]. Erevan, 2002, pp. 259–265 (in Russian).
7. Khubezhty Sh. S. Quadrature formulas for singular integrals with Cauchy kernel. Vladikavkazskii matematicheskii zhurnal = Vladikavkaz Mathematical Journal, 2008, vol. 10, no. 4, pp. 61–75 (in Russian).
8. Khubezhty Sh. S., Tsutsaev A. O. Quadrature formulas for singular integrals with nearly Gaussian degree of accuracy. Izvestiya vuzov. Severo-Kavkazskii region. Estestvennye nauki = Bulletin of Higher Education Institutes North Caucasus Region. Natural Sciences, 2015, no. 2, pp. 53–57 (in Russian).
9. Rusak V. N. Uniform rational approximation of singular integrals. Vestsі Natsyyanalʼnai akademіі navuk Belarusі. Seryya fіzіka-matematychnykh navuk = Proceedings of the National Academy of Sciences of Belarus. Physics and Mathematics series, 1993, no. 2, pp. 22–26 (in Russian).
10. Boksha A. N. Approximation of singular integrals by rational functions in the uniform metric. Vestnik Belorusskogo gosudarstvennogo universiteta. Seriya 1: Fizika, Matematika, Informatika [Bulletin of the Belarusian State University. Series 1: Physics, Mathematics, Computer Science], 1997, no. 3, pp. 68–71 (in Russian).
11. Rusak V. N., Uazis A. Kh. Rational approximation of singular integrals with differentiable density. Vestsі BDPU. Seryya 3. Fіzіka. Matematyka. Іnfarmatyka. Bіyalogіya. Geagrafіya [Bulletin of BSPU. Series 3. Physics. Mathematics. Informatics. Biology. Geography], 2009, no. 1(59), pp. 8–11 (in Russian).
12. Motornyi V. P. Approximation of Certain Classes of Singular Integrals by Algebraic Polynomials. Ukrainian Mathematical Journal, 2001, vol. 53, pp. 377–394. https://doi.org/10.1023/a:1012388120569
13. Rovba E. A. On one direct method in rational approximation. Doklady AN BSSR, 1979, vol. 23, no. 11, pp. 968–971 (in Russian).
14. Patseika P. G., Rouba Y. A., Smatrytski K. A. On one rational integral operator of Fourier–Chebyshev type and approximation of Markov functions. Journal of the Belarusian State University. Mathematics and Informatics, 2020, no. 2, pp. 6–27. https://doi.org/10.33581/2520-6508-2020-2-6-27
15. Potseiko P. G., Rovba E. A. Approximations on classes of poisson integrals by Fourier–Chebyshev rational integral operators. Siberian Mathematical Journal, 2021, vol. 62, no. 2, pp. 292–312. https://doi.org/10.1134/s0037446621020099
16. Lungu K. N. On the best approximations of possible functions with a fixed numerical pole. Mathematics of the USSRSbornik, 1971, vol. 86, no. 2, pp. 314–324. https://doi.org/10.1070/sm1971v015n02abeh001547
17. Lungu K. N. Best approximations by rational functions with a fixed number of poles. Siberian Mathematical Journal, 1984, vol. 25, pp. 289–296. https://doi.org/10.1007/bf00971467
18. Newman D. I. Rational approximation to |x|. Michigan Mathematical Journal, 1964, vol. 11, no. 1, pp. 11–14. https://doi.org/10.1307/mmj/1028999029
19. Potseiko P. G., Rovba Y. A. On Estimates of Uniform Approximations by Rational Fourier–Chebyshev Integral Operators for a Certain Choice of Poles. Mathematical Notes, 2023, vol. 113, pp. 815–830. https://doi.org/10.1134/s0001434623050231
20. Potseiko P. G., Rovba Ye. A. Conjugate Rational Fourier–Chebyshev Operator and its Approximation Properties. Russian Mathematics, 2022, vol. 66, pp. 35–49. https://doi.org/10.3103/s1066369x22030094
Review
Views: 352
Email this article 